Bayesian model comparison
With few information one can estimate how likely the outcome of a test for a disease is. Let $M$ denote that a patient has a particular disease and $M^\prime$ that he does not. And a test produces the outcome $D$, a postive or negative result.
\(P(D) = P(D,M)+P(D, M')\) Where $P(D,M)$ denotes the probability that $D$ and $M$ are true, $P(D,M^\prime)$ denotes the probability that $D$ and $M^\prime$ are true. \(P(D) = P(D\mid M)P(M)+P(D\mid M^\prime)P(M^\prime)\)
We would like to know what is the probability for having the disease given the test is positive $P(M \mid D)$.
\[P(M \mid D) = \frac{P(D \mid M)P(M)}{P(D)}\]with the previous definition of $P(D)$ we can simplify and the equation becomes.
\(P(M \mid D) = \frac{1}{1+1/R}\) with \(R = \frac{P(D \mid M)P(M)}{P(D \mid M^\prime)P(M^\prime)}\) which is the $\textit{posterior odds ratio}$.
| Probabilities | Values | Description |
|---|---|---|
| $P(D \mid M)$ | $0.95$ | True positive rate of the test |
| $P(M)$ | 0.009 | Prior probability having the disease |
| $P(D \mid M^\prime)$ | False positive rate of the test | |
| $P(M^\prime)$ | $1-P(M)$ | Not having the disease |
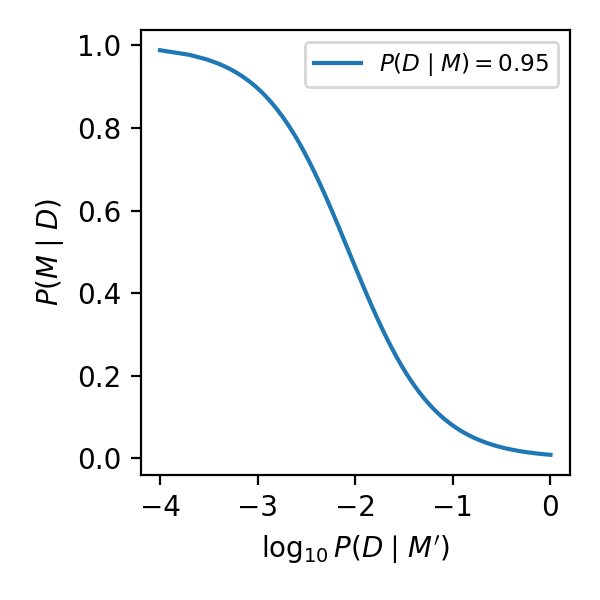
The following graph shows $P(M \mid D)$ as a function of $P(D \mid M^\prime)$. We can see that the test gets more reliable when the false positive rate drops.